Lasersköld

#teknik

Finding maximum correction for three samples

I always recalculate this when I need it, but now it is time to save it somewhere.

You have three samples y₁, y₂, and y₃, and you want to know where the maximum is, if you do a quadratic regression from it. We assume that the distance between the points on the x-axis is 1.

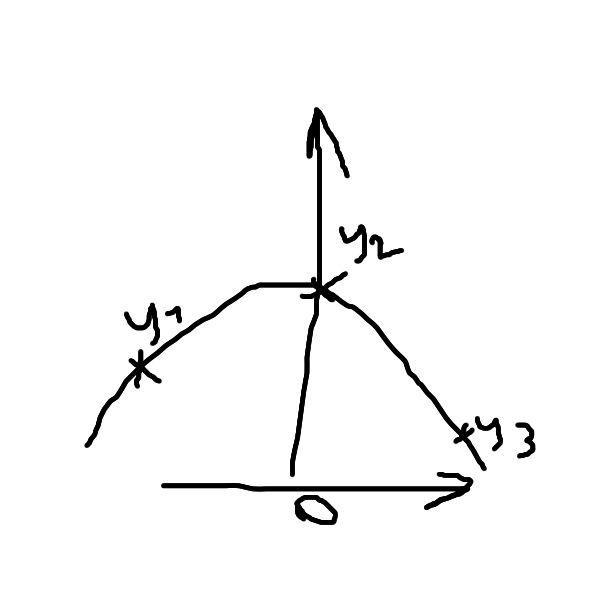
First, let's do the quadratic regression.

We describe the graph as:

$y=a{x}^2+bx+c$

So we want the values of a, b, and c.

For y₂ = y(x = 0), we have:

$y_2=a·0x^2+b·0+c$

Therefore, c = y₂.

We then have that:

$y_1=y(-1)=a·(-1)2^{)}$

This simplifies to:

$y_1=a-b+y_2$

Similarly, for y₃, we have:

$y_3=y\left(1\right)=a+b+y_2$

Now subtracting:

$y_3-y_1=2b$

Therefore:

b = (y₃ - y₁) / 2

Also, adding:

$y_1+y_3=2a+2y_2$

Thus:

$2a=y_1+y_3-2y_2$

a = (y₁ + y₃) / 2 - y₂

Now, to find the maximum, we take the derivative y':

$y=a{x}^2+bx+cy\text{'}=2ax+b$

Setting the derivative to zero for the maximum:

$0=2ax+b$

Substitute a and b:

$2((y_1+y_3)/2-y_2)x=-(y_3-y_1)/2$

Solve for x:

$x=(y_1-y_3)/(y_1+y_3-2y_2)/2$

... Done once and for all.

---

Andra inlägg från bloggen

2024

Använda cpp som ett skriptspråk (2024-12-03)

Mekaniskt tangentbord Lasersköld L1 del 1 (2024-11-14)

Alphasmart neo 2 font editor (2024-10-11)

Bloggen är äntligen fyttad (2024-09-24)

2022

Figurer i skuggan (2022-06-04)

2018

prestandatest pa morgonen c (2018-11-21)

2017

Framsteg och frustration (2017-08-31)

2015

fix audacity startup bug on ubuntu 1510 (2015-11-24)

git subtree (2015-06-21)

add native code to android studio (2015-06-21)

2014

Ingenting (2014-11-08)

Äldre inlägg...